Parameters of Cosmology: Microwave Background Polarization

 

Another Window into the Early Universe

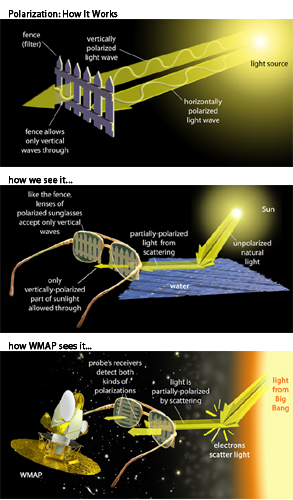
WMAP measures not only temperature fluctuations in the microwave background, but also the polarization of the microwave background. Theoretical models predict that it should exist at an amplitude detectable with WMAP's sensitivities. Multiple passes of the WMAP detectors across the sky have finally detected a faint microwave background polarization signal.

Scattered light, whether it is sunlight reflected off of haze, or microwave background photons that are reflected off of free electrons in the early universe is often polarized. This effect occurs because the electron-photon scattering cross-section depends upon the polarization of the incoming photon (which corresponds to the direction of the photon electric field). Because of this effect, we can probe the properties of the electrons that the photon encounters as it propagates from the surface of last scatter to our experiment.

At this point in the discussion, the astute reader might object, "but wait, I thought that there were no free electrons left once the universe cooled below 3000 K". Fortunately, this is not true. Once stars start forming their radiation will ionize hydrogen, thus liberating free electrons. These free electrons will produce polarization fluctuations in the microwave background that are detectable.

< Back to Overview Beginning